|
Math should be fun and engaging! We have to change our instructional methods to engage the digital native population. As a reward based on assessment performance Warrior Math uses Kahoot.it as a formative assessment tool in the classroom. My mission is to help students think like mathematicians and to be able to persevere in problem solving. Our daily tools and strategies include close reading, annotation skills, writing in math journals, and problem-solving, contextualization, decontextualization of passages, using tools to deepen our understanding of math and the outside world. But sometimes we need something to be fun, engaging, and learning math at the same time. During the next few weeks this blog will be introducing exactly how we are using technology to enhance learning of mathematics.
0 Comments
The daily journal instructional guidance is now spreading to other content areas by the students in my Warrior Math Class. The next step is to get students to move from answering Domain of Knowledge (DOK) levels 1 & 2 to do more of DOK levels 3 & 4 thinking.
Accountability versus Learning
Co-Teaching works and "All Means All" students can learn with the right instructional methods done consistently. Every student needs to know what they are learning on a daily basis. But most importantly they need to know why they are learning and why it is important to them that they do well. One solution is to have students write on a daily basis in a journal but as a minimum to summarize what they have learned on a daily basis. Using the blended model approach we can enhance learning and share with other students. Students need to talk about the topic and this is so true in learning mathematics. Below is a daily post from one of the students in the Warrior Math Classroom. Interesting enough is my conversation with one of my new students just two weeks ago: I heard these common statements, "I'm not good at math", " I hate math", " Math sucks", and the list goes on and on. Below are the comments from that same student after two weeks in my Warrior Math classroom. Understanding the importance of mathematical discourse and talking about mathematical concepts allows students to reflect on their own understanding while making sense of and critiquing the ideas of others. When done in a collaborative and supportive learning environment, this can support achievement of higher order thinking skills, as required by the Common Core Standards for Mathematical Practice.
Students can make conjectures, link prior knowledge to current understanding, reason about mathematics, refine and amend their approaches, and take ownership of their mathematical knowledge. Students benefit greatly from learning to use the tools of mathematical discourse—including words, symbols, diagrams, physical models, and technology—to present and defend their ideas. Imparting these new skills on students allows teachers to access, monitor, and evaluate students’ mathematical understanding and development. ASSESSMENT Students need the opportunity to practice an assessment prior to it counting for a grade. Feedback about their progress in learning is more valuable than receiving a test back with a letter grade. In the Warrior Math Classroom there are not grades of "D" or "F" because this is not a positive reflection of what is important. Each student has a status of learning on a daily basis. EVIDENCE OF LEARNING Warriors use posters to illustrate and share about their learning of mathematical concepts. Warriors write in their math journals every day. How does the teacher know on a daily basis what students are learning and if they got it? Our solution is to simply ask them to write about it in their math journals. After two days of doing this we discover there is one more question to ask each and every day? Can you figure out what is the most important question not on the above list. This post was done by a student who previously had no experience or success in learning math. A growth mindset can change anyone!
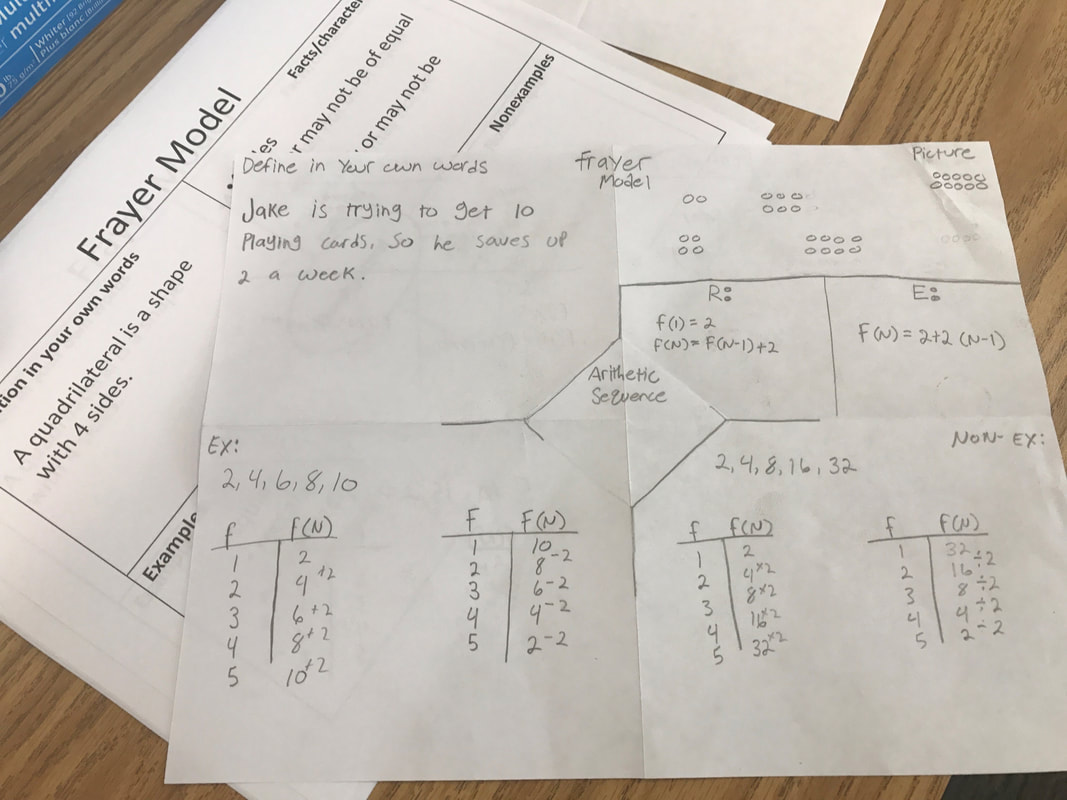
Purpose: The purpose of this task is to practice writing recursive and explicit formulas for arithmetic and geometric sequences from a table. This task also provides practice in using tables to identify when a sequence is arithmetic, geometric, or neither. The task extends students’ experiences with sequences to include geometric sequences with alternating signs, and more work with fractions and decimal numbers in the sequences.
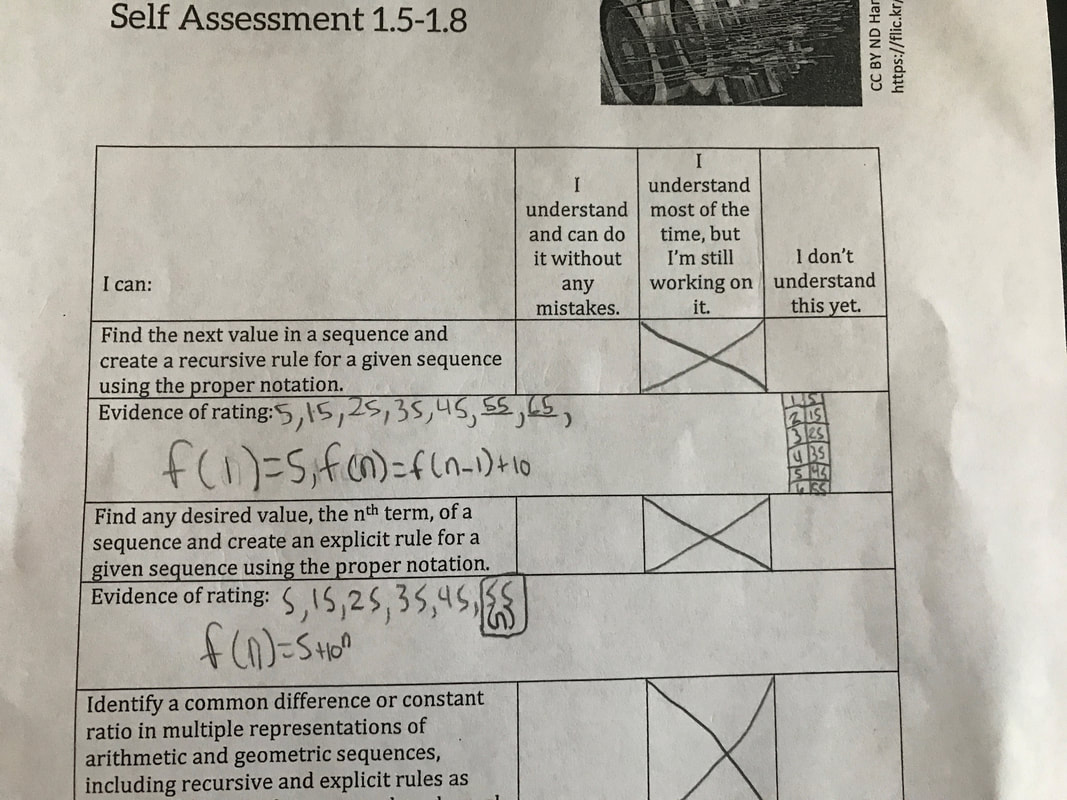
Standards for Mathematical Practice of Focus in the Task: SMP7 – Look for and make use of structure. MP8 – Look for and express regularity in repeated reasoning. Students receive feedback to self-assess their learning by responding:
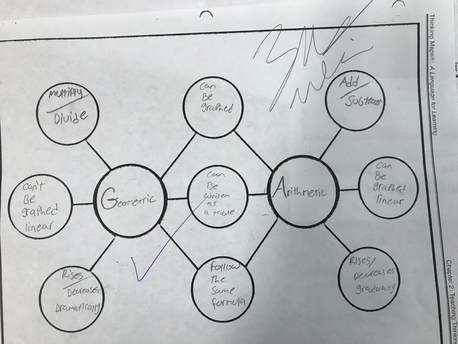
The purpose of this task is to solidify and extend the idea that geometric sequences have a constant ratio between consecutive terms to include sequences that are decreasing (0 < r < 1). The common ratio in one geometric sequence is a whole number and in the other sequence it is a percent. This task contains an opportunity to compare the growth of arithmetic and geometric sequences. This task also provides practice in writing and using formulas for arithmetic sequences.
Standards for Mathematical Practice SMP7 – Look for and make use of structure. SMP6 – Attend to precision. Students receive feedback to self-assess their learning by responding:
POSITIVE Feedback Works: I spent the afternoon calling parents with good news about students performance in my classroom. Twenty-five percent of the students had a score of 100%, 87% scored 75% or better. Those scoring less than 75 % received immediate two days of extra support. This new approach for teaching mathematics in an alternative school is improving instruction and staff collaboration. The student outcomes for the school community correlates positively assimilating an exponential growth function about learning mathematics for all students. Objective: Show your thinking and providing evidence of learning using graphic organizing thinking tools. Principles to Action recommends that students be able to make connections with mathematics through the use of multiple representations. Formative assessment allows students and teachers to assess learning and understanding of mathematics. Conceptual understanding is the foundation for permanent learning of mathematics and the ability to think like a mathematician (NCTM, 2014). The following tools are necessary to demonstrate comparing and contrasting the similarities between sequences and to clearly demonstrate understanding of a mathematical concept (SMP 1-7).
|
Dr. Smith
|
- Home
- CAASPP/SBAC PREP
- Orientation
- Dr. Smith MATH BLOG-2017-2018
- Privacy Policy
- Hour of Code
- Math Fun Night Videos
- CCHS MATH I
- CCHS MATH II
- CCHS MATH III
- Art of Math
- Parents
- RTI-FLOWMAP
- WOF-Good
- Hourofcode
- Content Objectives
- Common Core Standards
- Geometry Proofs
- MusicBlog
- CCHS Kahoot Challenge
- MATH & PEOPLE
- JavaScript Programming
- Star Wars
- Pearson Video Help
- Conference Presentations
- SBAC Practice #1
- SJAE Exit Survey
- CCEA MATH Resources
- CCHS MATH BLOG-2018-2019
- Brain-Based Research
- Stock Market Game



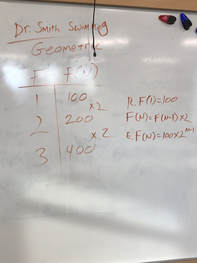






 RSS Feed
RSS Feed
